Пригласи друга на ZaBeRa и заработай!

Начать зарабатывать

Полезные советы о том, как легко сократить сложные дроби и привести их к наименьшему общему знаменателю?

#хакнем_математика рубрика, содержащая интересный, познавательный контент по математике как для школьников, так и ...

Иллюстрация защищена товарным знаком и принадлежит медиа-группе «Хакнем»

Цикл статей "Дроби"

Первая часть Вторая часть Третья часть Четвертая часть Пятая часть

Здравствуйте, уважаемые читатели!

Отмечу, что в одних учебниках материал этой статьи рассматривается в 5-ом классе, в других — в 6-ом. Прежде чем продолжить чтение этой статьи, предлагаю Вам познакомиться с пятой статьёй цикла «Признаки делимости чисел: где мы их применяем в жизни», автор которой #ирина_чудневцева любезно предоставила её в наше с Вами распоряжение.

Нахождение Наибольшего Общего Делителя (НОД) и Наименьшего Общего Кратного (НОК) двух чисел служит для преобразований обыкновенных дробей при их сокращениях или для приведения к общему знаменателю при сложении и вычитании.

При наличии достаточного опыта эти преобразования во многих случаях производятся «в уме» и довольно быстро приводят к нужному результату.

Однако так бывает далеко не всегда. При достаточно больших значениях как числителя, так и знаменателя сделать устно подобные преобразования достаточно затруднительно.

В таких случаях необходимо каждое из этих чисел разложить на простые множители. Именно при выполнении этой операции нам на помощь приходят признаки делимости.

Давайте подробно рассмотрим операцию сокращения дроби

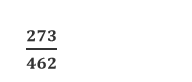
Полезные советы о том, как легко сократить сложные дроби и привести их к наименьшему общему знаменателю?

Запишем раскладываемое на простые множители число и справа от него проведём вертикальную черту, за которой запишем возможно наименьший простой делитель этого числа.

Результат деления запишем под первым числом, а его наименьший простой делитель — за чертой… Далее запишем частное от деления числа на простой множитель под самим числом, а его наименьший простой делитель — за чертой.

Продолжим этот процесс до появления в частном числа 1.

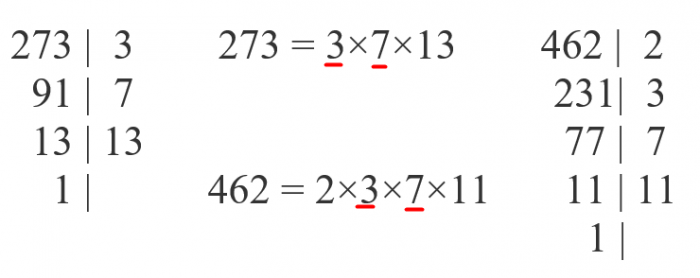
Полезные советы о том, как легко сократить сложные дроби и привести их к наименьшему общему знаменателю?

Отметим каким-либо способом (обычно это делается подчёркиванием) совпадающие множители в этих разложениях.

Произведение подчёркнутых множителей и будет наибольшим

общим делителем: НОД(273; 462) = 3 × 7 = 21.

ВНИМАНИЕ! Теперь для сокращения дроби нам нет нужды делить её числитель и знаменатель на найденный НОД!

В качестве числителя и знаменателя сокращённой дроби будут

произведения неотмеченных множителей в их разложениях:

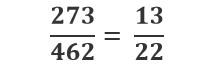
Полезные советы о том, как легко сократить сложные дроби и привести их к наименьшему общему знаменателю?

Пусть теперь эти числа (273 и 462) будут знаменателями каких-то обыкновенных дробей, которые следует привести к общему знаменателю. Не вызывает сомнений, что этот общий знаменатель должен быть наименьшим из всех возможных.

Таким Наименьшим Общим Знаменателем будет Наименьшее Общее Кратное (НОК) этих чисел.

НОК(273; 462) — это одно из этих чисел, умноженное на

произведение неотмеченных множителей в разложении другого

числа:

НОК(273; 462) = 273 × (2×11) = 462 × 13 = 6006.

Умножим числитель каждой дроби на неотмеченные простые множители в разложении на простых множителей знаменателя другой дроби — это будут дополнительные множители, и поставим полученное произведение в числитель приведённой к общему знаменателю дроби, а её знаменателем будет найденное значение НОК.

Осталось показать, что произведение двух чисел равно произведению НОД и НОК этих чисел, Сделаем это сначала в общем виде.

Пусть натуральное число M = AD, а натуральное число N = BD,

где D = НОД(M; N), A — произведение неотмеченных простых множителей в разложении числа M, B — произведение неотмеченных простых множителей в разложении числа N.

Тогда

mn = ad×bd, НОД(m; n) × НОК(m; n) = d × m × b = d × ad ×b = ad × bd= mn.

Предлагаю читателю самостоятельно убедится в справедливости

этого равенства при m = 273 и n = 462.

Если вам было интересно, не забудьте подписаться на наш канал и хэштег #хакнем_математика

Автор: #себихов_александр 71 год, много лет проработал конструктором-технологом микроэлектронных приборов и узлов в одном из НИИ г. Саратова, затем преподавателем математики и физики.

Канал Хакнем Школа благодарит нашего автора Себихова Александра Николаевича за познавательный контент и возможность опубликования его в нашем канале!

Другие статьи автора:

* Справитесь ли Вы с задачами Всероссийской олимпиады по математике 4-х классов?
* Нестандартная задача, развивающая смекалку и математическую интуицию
* Задачи на движение — головная боль школьников. Как научиться их решать?



Полезные советы о том, как легко сократить сложные дроби и привести их к наименьшему общему знаменателю?

Цикл статей "Дроби"

1 статья

2 статья

3 статья

4 статья

5 статья

6 статья [Текущая]

Контент создан при поддержке медиагруппы «Хакнем».